解数学方程表组答案

在这一可选部分中，我们将开发在上一个视频中介绍的解数学方程表组。 首先，我们将讲解二维情况，然后讲解一般情况。

二维情况的答案

我们的数据将会是值
x_1, x_2, \ldots, x_m,
而我们的标签将会是值
y_1,y_2, \ldots, y_n.
我们将权重记为
w_1,
和
w_2.
因此，我们的预测是
\hat{y_i} = w_1x_i + w_2.
平均平方误差是

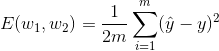
我们需要最小化误差函数。因此，
\frac{1}{m}
可以被忽略。现在替换
\hat{y},
值，我们得到

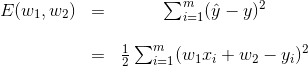
修正：上方公式中第一行缺少一个1/2。

现在，为了最小化这一误差函数，我们需要将
w_1
和
w_1
的导数设置为
0.

使用链式规则，我们得到

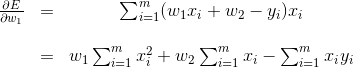
和

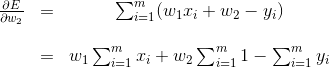
将以上两则公式设置为 0 ，我们得到一下两则公式和两个变量 （这里变量是
w_1
和
w_2)。

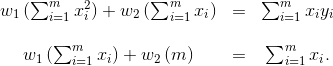
修正：上方第二行公式中最后的x_i应更改为y_i。

我们可以用任何方法来求解 2 个方程和 2 个变量。 例如，如果我们将第二个方程乘以
\sum_{i=1}^m x_i,
第一个乘以
m,
两者相减得到值
w_1,
然后在第一个方程中替换该值，我们得到如下结果：

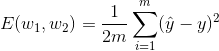
这是我们理想的答案。

n-维度情况下的答案

当我们的数据有n 个维度时，而不只是 2个，我们需要介绍一下的表示法。我们的矩阵
X
包含的数据如接下来所示，每一行都是我们的 datapoint， 在此
x_0^{(i)} =1
表示偏差。

我们的标签是向量

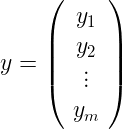
而我们的权重矩阵如下所示：

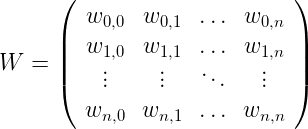
所以，平均平方误差的方程可写成如下矩阵乘积：

E(W) = \frac{1}{m} ((XW)^T - y^T) (XW - y).

因为我们需要最小化平均平方误差，我们可以先忘记
\frac{1}{m}, 展开公式，我们得到

E(W) = W^TX^TXW - (XW)^Ty - y^T(XW) + y^Ty.

注意在上面的总和中，第二和第三项是相同的，因为它是两个向量的内积，这意味着它是它的坐标乘积之和。 因此，

E(W) = W^TX^TXW - 2(XW)^Ty + y^Ty.

为了最小化，我们需要对矩阵中的所有值采取导数
W.使用上方我们使用的链式规则，我们得到以下结果：

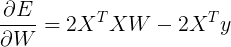
为了将这个设置为0，我们需要

X^TXW - X^Ty = 0,
或者等同于，

W = (X^TX)^{-1} X^T y.

这就是我们解数学方程表组答案
W!
正如我们在视频中所述，这种方法在现实生活中将会很昂贵而不实用，因为要找到矩阵的倒数
X^TX很难，如果是在
n
很大的情况下。 这就是我们需要经历多次梯度下降的痛苦的原因。 但是，如果我们的数据稀疏，即如果矩阵的大部分条目
X
是 0，就会有一些非常有趣的算法，能够迅速找到这个倒数，将使这种方法在现实生活中非常有用。